Skip to main content

距离-多普勒模型

R-D模型公式推导

公式总览​

Rj2=(RS⃗−RT⃗)2fd=2λ(RS⃗−RT⃗)VS∣RS⃗−RT⃗∣\begin{align} {Rj}^2 =& (\vec{R_S}-\vec{R_T})^2 \\ f_d =& \frac{2}{\lambda}\frac{(\vec{R_S}-\vec{R_T})V_S}{\lvert\vec{R_S}-\vec{R_T} \rvert} \end{align}

式中， RjR_j为卫星, SS到地物点, TT的斜距, RSR_S是卫星的位置矢量, RTR_T是地物点的位置矢量。

公式推导​

距离方程​

多普勒方程​

对于SAR，整个过程分为两个阶段

  1. 卫星发出信号，地物接收

    视SAR为声源，地物为观察者。 声源向着观察者方向移动，观察者不动。

  2. 地物反射信号，卫星接收

    视地物为声源，SAR为观察者。 声源不动，观察者移动。

设SAR发射的电磁波频率为 f0f_0，1.中地物接收的频率为 f′f'，2.中卫星接收的频率为 ff，则有

f′=cc−w′f0f=c+w′cf′\begin{align} f'=& \frac{c}{c-w'}f_0 \\ f =& \frac{c+w'}{c}f' \end{align}

其中， cc为光速， w′=wcos⁡ψw'=w\cos\psi， ww为卫星速度矢量， ψ\psi为方位角。

公式原理参考多普勒效应。

所以，多普勒频移

Δf=f−f0=(c+w′c−w′−1)f0=2w′c−w′f0≈2w′λ=2λ⋅dRdt\begin{aligned} \Delta f =& f - f_0 \\ =& (\frac{c+w'}{c-w'}-1)f_0 \\ =& \frac{2w'}{c-w'}f_0 \\ \approx& \frac{2w'}{\lambda} = \frac{2}{\lambda}\cdot \frac{dR}{dt} \end{aligned}

其中， w′w'为 ww在 TS→\overrightarrow{TS}方向的分量， R=(XS−XT,YS−YT,ZS−ZT)⋅(±1)R=(X_S-X_T,Y_S-Y_T,Z_S-Z_T)\cdot(\pm1)

w′=dRdt=±d(XS−XT)2+(YS−YT)2+(ZS−ZT)2/dt=±(XS−XT)(VSX−VTX)+(YS−YT)(VSY−VTY)+(ZS−ZT)(VSZ−VTZ)(XS−XT)2+(YS−YT)2+(ZS−ZT)2∵Vt=0∴w′=dRdt=±(RS⃗−RT⃗)VS⃗∣RS⃗−RT⃗∣\begin{aligned} w'= \frac{dR}{dt} =& \pm d\sqrt{(X_S-X_T)^2+(Y_S-Y_T)^2+(Z_S-Z_T)^2}/dt \\ =& \pm \frac{(X_S-X_T)(V_{SX}-V_{TX})+(Y_S-Y_T)(V_{SY}-V_{TY})+(Z_S-Z_T)(V_{SZ}-V_{TZ})}{\sqrt{(X_S-X_T)^2+(Y_S-Y_T)^2+(Z_S-Z_T)^2}} \\ \because V_t =& 0 \\ \therefore w' =& \frac{dR}{dt} = \pm \frac{(\vec{R_S}-\vec{R_T})\vec{V_S}}{\lvert \vec{R_S}-\vec{R_T} \rvert} \end{aligned}

综上所述,

Δf=2λ(RS⃗−RT⃗)VS⃗∣RS⃗−RT⃗∣\begin{align} \Delta f = \frac{2}{\lambda}\frac{(\vec{R_S}-\vec{R_T})\vec{V_S}}{\lvert \vec{R_S}-\vec{R_T} \rvert} \end{align}

多普勒效应​

多普勒效应是RD模型中，多普勒方程的基础。

观察者 AA，声源 SS. 观察者移动速度为 vAv_A，声源移动速度为 vSv_S，波的速度和频率分别为 vv和 ff。

1.观察者移动，声源不动​

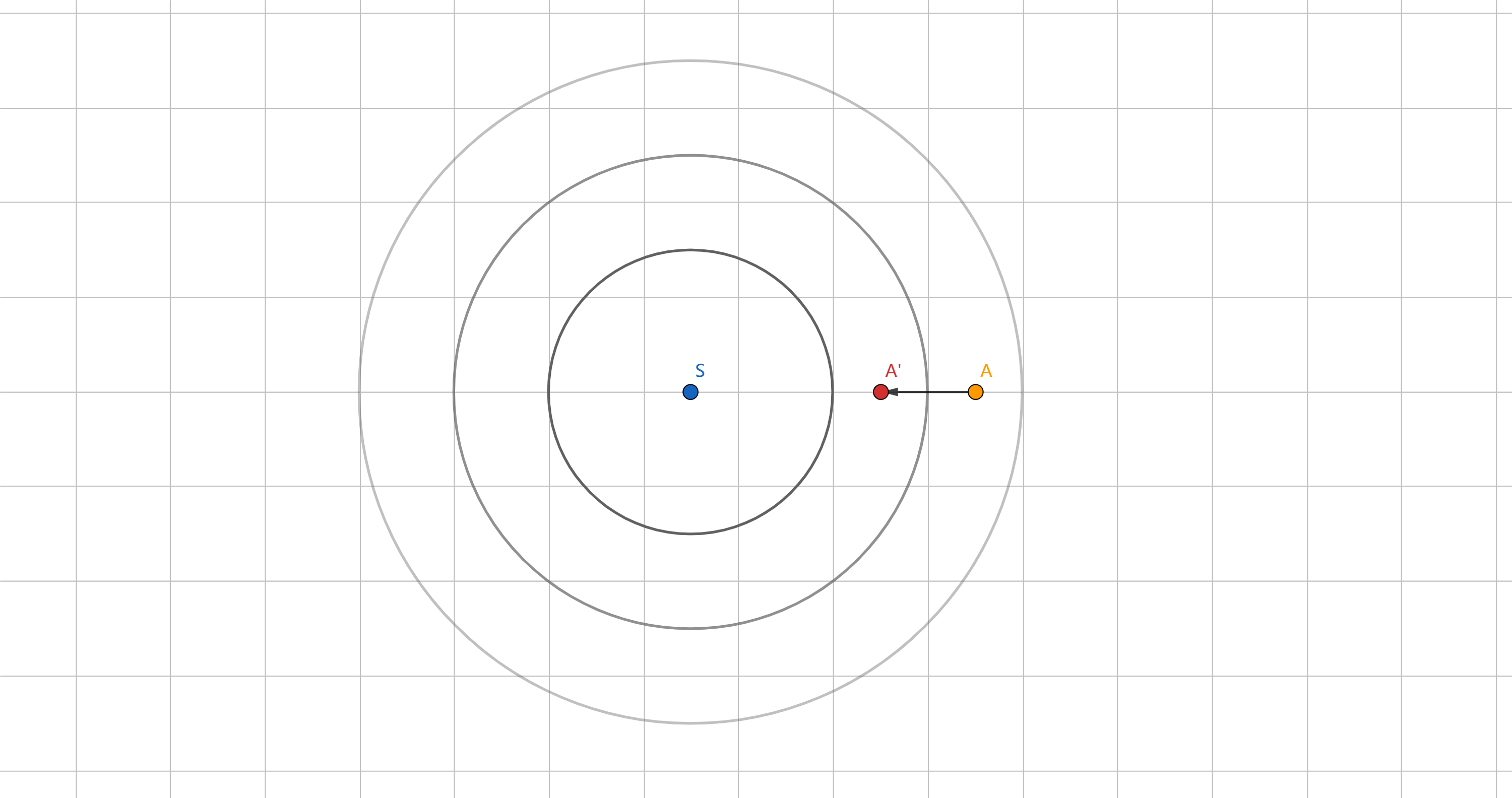
观察者移动 生源不动

当 AA移动到 A′A'时，走过距离 vAtv_At，声传播距离 vtvt.

所以， AA经历的波数 NN等于 (vA+v)t(v_A+v)t除以波长 λ\lambda，即

N=vAt+vtλN=\dfrac{v_At+vt}{\lambda}

波数 NN除以时间 tt，即为单位时间的波数，等效为频率

f′=vAt+vtλt=vA+vλ=v+vAvf>f\begin{aligned} f'=& \frac{v_At+vt}{\lambda t}\\ =& \frac{v_A+v}{\lambda } \\ =& \frac{v+v_A}{v}f > f \end{aligned}

由上可知，当观察者 AA向波源 SS移动时，接收到的频率 f′f'大于波源发出的频率 ff。反之，逃离时则小于。

2.声源移动，观察者不动​

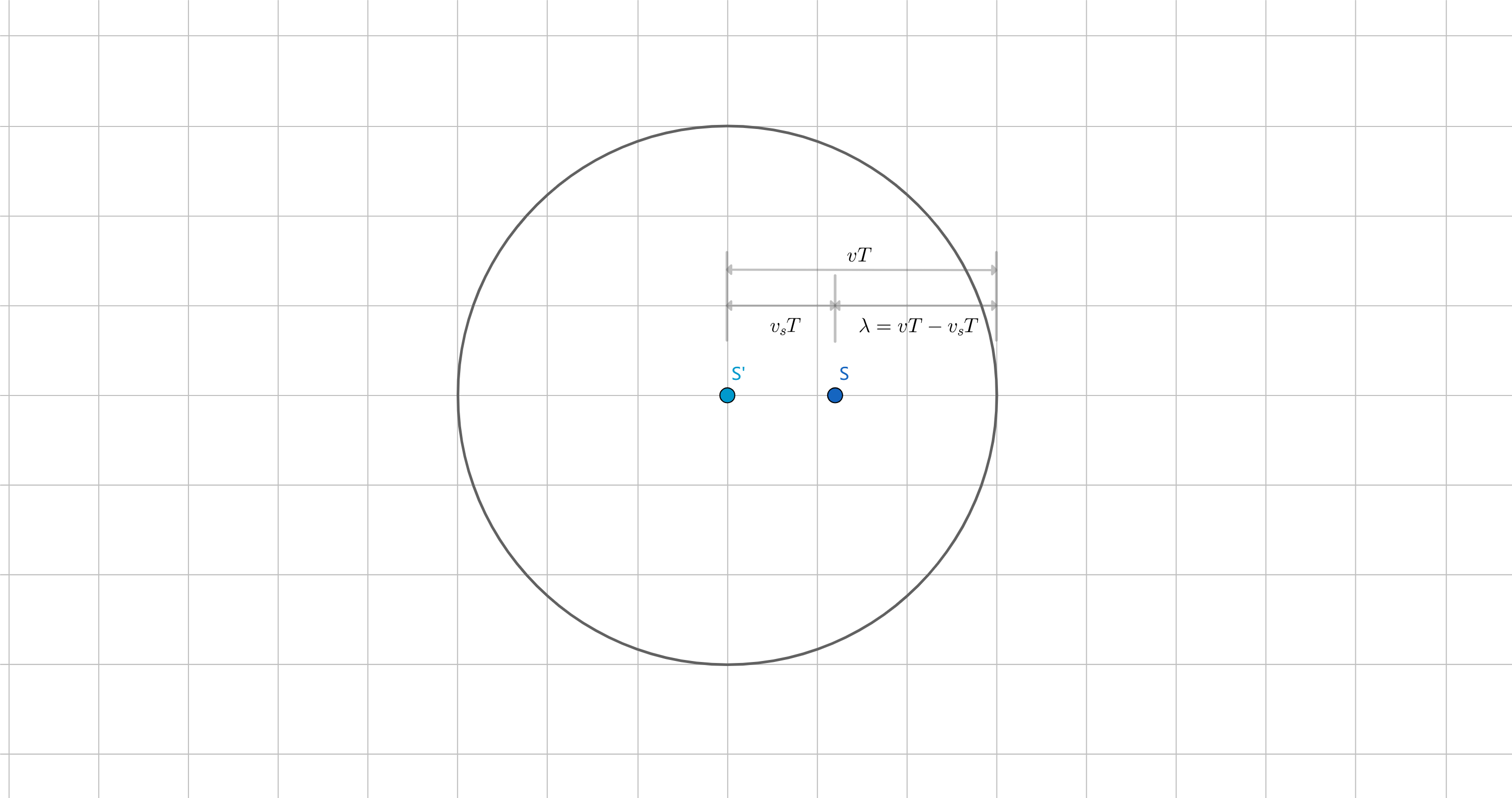
声源移动 波长改变

已知 f=1Tf=\dfrac{1}{T}， TT为发射一个波所需要的时间， TT时间内，博得传播速度为 vTvT，波源的移动距离为 vSTv_ST. 此时，波源 SS到波的距离即为波长,

λ=vT−vST\lambda = vT-v_ST

认为当波源 SS向观察者 AA移动时，波长 λ\lambda缩短。

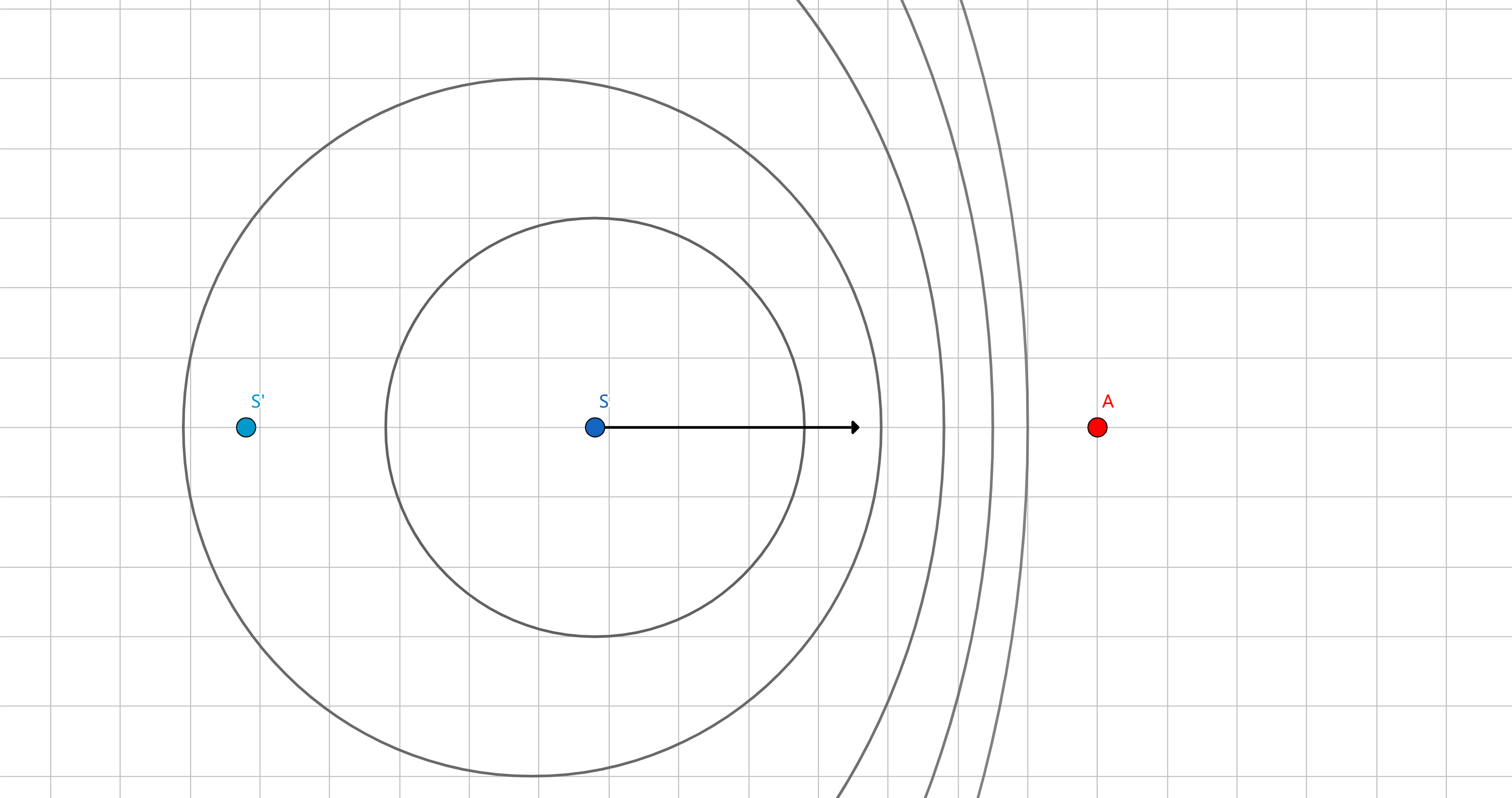
声源移动 观察者不动

以观察者接受到声波为起始时间，共精力时间 tt，此时波的传播距离为 vtvt，除以波长得到波数（ AA接收到波的个数）

N′=vtλ=vtvT−vST=vtv−vSfN'=\frac{vt}{\lambda}=\frac{vt}{vT-v_ST}=\frac{vt}{v-v_S}f

波数 N′N'除以时间 tt，即为单位时间接收到的声波个数，等效为频率

f′=vtv−vSft=vv−vSf>ff'=\frac{\frac{vt}{v-v_S}f}{t}=\frac{v}{v-v_S}f > f

所以，当声源向观察者移动时（ vS>0v_S>0），接收到的频率 f′f'大于波源的发出频率 ff，反之则小于。

零化处理的猜想​

根据多普勒效应可知，

卫星发射信号阶段，如果卫星向地物方向移动，会导致地物接收的信号频率大于卫星发射频率，即f′>f0f'>f_0,

卫星接收反射信号阶段，如果卫星原理地物，会导致卫星接收的信号频率小于地物反射频率，即f>f′f>f',

已知卫星在某时刻的速度矢量为VS⃗\vec{V_S}, 卫星发射信号时面向地物方向运动，接收信号时远离地物方向运动，此时卫星发射ff与接收f0f_0的信号频率关系为,

f=cc−w′f′=cc−w′⋅c+(−w′)cf0=f0\begin{aligned} f =& \frac{c}{c-w'}f' \\ =& \frac{c}{c-w'} \cdot \frac{c+(-w')}{c} f_0 \\ =& f_0 \\ \end{aligned}

式中，w′w'为速度矢量的模 ∣VS⃗∣\lvert \vec{V_S} \rvert。

所以，这种情况下，多普勒频移Δf=0\Delta f = 0, 即为零化多普勒处理。

（猜想...）