Skip to main content

基于RD模型的坐标转换

i,j,h->lat,lon​

通过指定的斜距 rhorho和轨道位置矢量 ss, vv计算出其对应的大地坐标 latlat, lonlon

代码涉及点和向量信息如下图所示，

几何关系

代码实现​

/// class llh{
///   double longitude, latitude, height; 
///   xyz to_xyz(); // 转换到空间直角坐标系
///   //...
/// };
/// class xyz{
///   double x, y, z; 
///   double norm(); // 取模
///   xyz cross(xyz sec); //外积, 叉乘
///   xyz operator-(xyz sec); //向量相减
///   xyz operator+(xyz sec); //向量相加
///   double operator*(xyz sec);  //内积, 点乘
///   xyz operator*(double m);  // 向量乘常数
///   llh to_llh(); // 转换到经纬度
///   //...
/// };

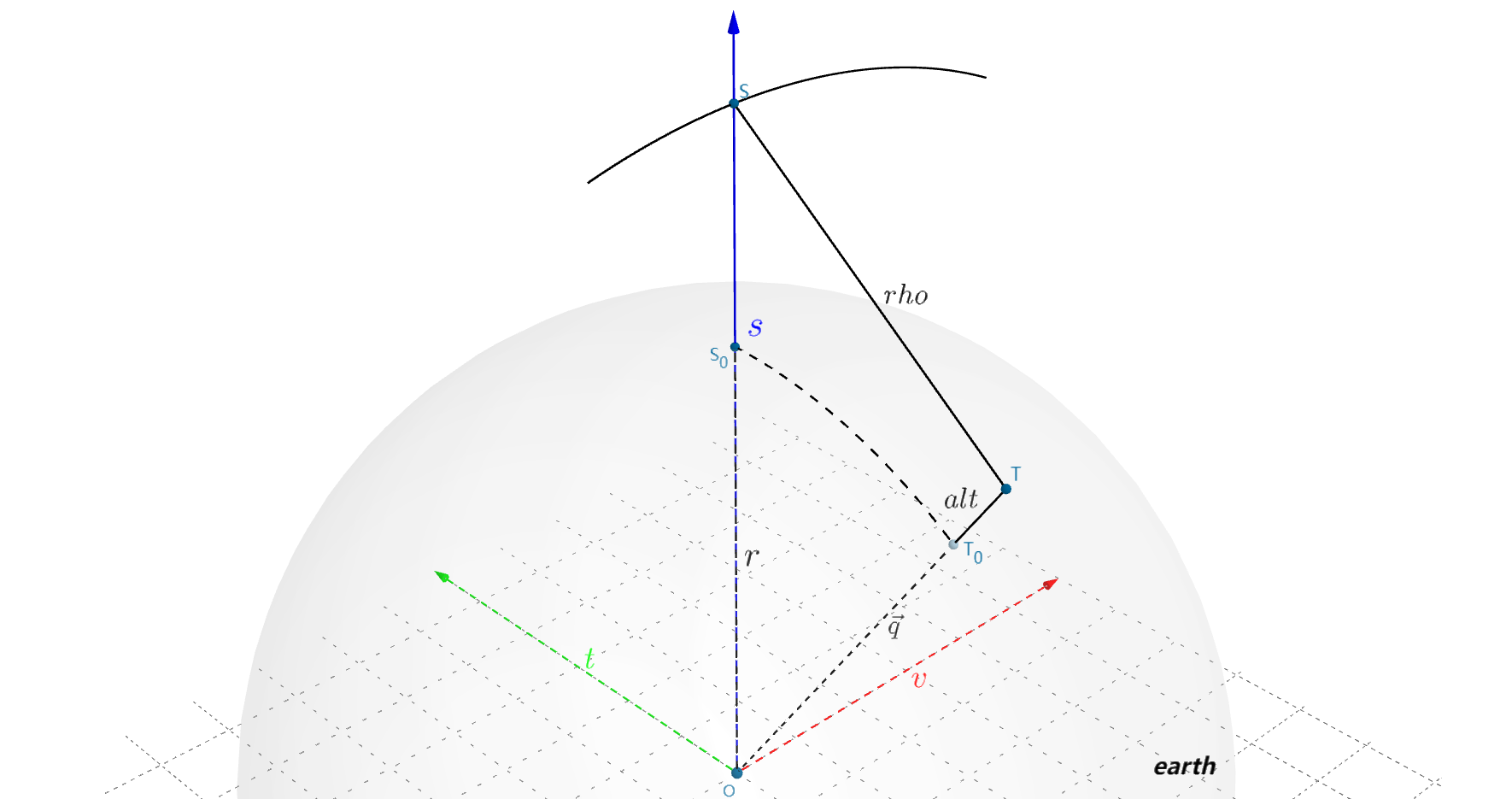
llh parameter_sar::get_target_loc(double az_row, double sr_col, double alt)
{
    double C = 299792458; //光速
    double rho = this->get_slant_range(sr_col);   //计算斜距
    
    double fc = radar_frequency;
    int s_flag = (look_direction == Look_Diredction::right)?-1:1; //左右视
    double state_t = this->get_azimuth_time(az_row); //根据简单比例关系估计方位向时间 state_t = az_start + azTimeSpacing * az_row
    double fd = 0;
    if (!azimuth_deskew) {
        fd = get_fd(state_t, rho); // 计算多普勒频移
    }
    xyz s = this->get_state_pos(state_t );
    xyz v = this->get_state_velo(state_t );

    llh dst;
    double a, b, c, r, r1, lam;
    double s2, v2, t2, sv, det;
    double lat1, lon1, alt1, c1, c2, c3;
    double r_new;
    xyz q, t;
    int iter;

    lam = C / fc;
    s2 = s * s;
    v2 = v * v;
    sv = v * s;
    llh temp = s.to_llh();
    lon1 = temp.longitude;
    lat1 = temp.latitude;
    alt1 = temp.height;

    r = sqrt(s2) - alt1;
    t = s.cross(v);
    t2 = t * t;

    iter = 0;
    while (iter < 17 )
    {
      iter++;

      a = (s2 + SQR(r + alt) - SQR(rho)) / 2.0;
      b = (lam * rho * fd + 2.0 * sv) / 2.0;
      c = SQR(r + alt);

      det = s2 * v2 - SQR(sv);

      c1 = (a * v2 - b * sv) / det;
      c2 = (b * s2 - a * sv) / det;
      c3 = double(s_flag) * sqrt((c - pow(c1,2) * s2 - pow(c2,2) * v2 - 2.0 * c1 * c2 * sv)/t2);

      /*  radius vector to image point is q = c1*s + c2*v + c3*t */
      q = s * c1 + v *c2 + t * c3;

      llh temp2 = q.to_llh();
      lon1 = temp2.longitude;
      lat1 = temp2.latitude;
      alt1 = temp2.height;

      r1 = q.norm();        /* includes surface altitude of alt1, earth radius=r1-alt1 */
      r_new = r1 - alt1;
      if (fabs(r_new - r) < .001)
          break;
      r = r_new;
    }

    dst.latitude = lat1;
    dst.longitude = lon1;
    dst.height = alt;

    return dst;
}

以无误差值推算公式​

代码中的a和b和det可以进一步推导得到：

a=s2+q2−rho22=∣s∣∣q∣cos(∠soq)b=λ⋅rho⋅fd+2⋅sv2=q⋅vdet=s2v2−(sv)2=∣s∣2∣v∣2−∣s∣2∣v∣2cos2(∠sov)=∣s∣2∣v∣2sin2(∠sov)=∣t∣2\begin{aligned} a ={}& \frac{s^2+q^2-rho^2}{2}\\ ={}&\lvert s \rvert \lvert q \rvert cos(\angle soq) \\\\ b ={}&\frac{\lambda \cdot rho \cdot fd + 2 \cdot sv}{2}\\ ={}& q \cdot v \\\\ det = {}&s^2v^2-(sv)^2 \\ = {}&\lvert s\rvert^2\lvert v\rvert^2-\lvert s\rvert^2\lvert v\rvert^2cos^2(\angle sov) \\ = {}&\lvert s\rvert^2\lvert v\rvert^2sin^2(\angle sov) \\ = {}&\lvert t\rvert^2 \\\\ \end{aligned}

这里将 r+altr+alt等效为 ∣q∣\lvert q \rvert ，但实际上两者存在一定误差，下一节在讨论该问题。

分别带入 c1c_1和 c2c_2，得到：

c1=a⋅v2−b⋅svdet=∣s∣∣q∣cos(∠soq)∣v∣2−∣q∣∣v∣cos(∠qov)∣s∣∣v∣cos(∠sov)∣s∣2∣v∣2sin2(∠sov)=∣q∣cos(∠soq)−∣q∣cos(∠qov)cos(∠sov)∣s∣sin2(∠sov)c2=b⋅s2−a⋅svdet=∣q∣∣v∣cos(∠qov)∣s∣2−∣s∣∣q∣cos(∠soq)∣s∣∣v∣cos(∠sov)∣s∣2∣v∣2sin2(∠sov)=∣q∣cos(∠qov)−∣q∣cos(∠soq)cos(∠sov)∣v∣sin2(∠sov)\begin{aligned} c_1=&\frac{a\cdot v^2-b\cdot sv}{det}\\ =&\frac{\lvert s\rvert\lvert q\rvert cos(\angle soq)\lvert v\rvert^2-\lvert q\rvert\lvert v\rvert cos(\angle qov)\lvert s\rvert\lvert v\rvert cos(\angle sov)}{\lvert s\rvert^2\lvert v\rvert^2 sin^2(\angle sov)} \\ =&\frac{\lvert q\rvert cos(\angle soq)-\lvert q\rvert cos(\angle qov) cos(\angle sov)}{\lvert s\rvert sin^2(\angle sov)} \\ c_2=&\frac{b\cdot s^2-a\cdot sv}{det}\\ =&\frac{\lvert q\rvert\lvert v\rvert cos(\angle qov)\lvert s\rvert^2-\lvert s\rvert\lvert q\rvert cos(\angle soq)\lvert s\rvert\lvert v\rvert cos(\angle sov)}{\lvert s\rvert^2\lvert v\rvert^2 sin^2(\angle sov)} \\ =&\frac{\lvert q\rvert cos(\angle qov)-\lvert q\rvert cos(\angle soq) cos(\angle sov)}{\lvert v\rvert sin^2(\angle sov)} \\ \end{aligned}

如果近似的认为 ∠sov≈90°\angle sov \approx 90 \degree，则有，

cos(∠sov)≈0sin(∠sov)≈1\begin{aligned} cos(\angle sov) \approx 0 \\ sin(\angle sov) \approx 1 \end{aligned}

从而得到 c1c_1和 c2c_2的近似值：

c1=∣q∣cos(∠soq)∣s∣c2=∣q∣cos(∠qov)∣v∣\begin{aligned} c_1 = & \frac{\lvert q\rvert cos(\angle soq)}{\lvert s\rvert} \\ c_2 = & \frac{\lvert q\rvert cos(\angle qov)}{\lvert v\rvert} \\ \end{aligned}

同理，得到 c3c_3:

c3=±q2−c12s2−c22v2−2c1⋅c2⋅svt2=±q2−∣q∣2cos2(∠soq)−∣q∣2cos2(∠qov)∣t∣=±∣q∣cos(∠qot)∣t∣\begin{aligned} c_3 =& \pm\sqrt{\frac{q^2-c_1^2s^2-c_2^2v^2-2c_1\cdot c_2\cdot sv}{t^2}} \\ =& \pm \frac{\sqrt{q^2 - \lvert q \rvert^2 cos^2(\angle soq)-\lvert q \rvert^2 cos^2(\angle qov)}}{\lvert t \rvert} \\ =& \pm \frac{\lvert q\rvert cos(\angle qot)}{\lvert t\rvert} \\ \end{aligned}

可知， c1c_1、 c2c_2、 c3c_3分别为向量q的单位向量在 ss、 vv、 tt坐标轴上的分量，所以有：

q=c1⋅s+c2⋅v+c3⋅tq = c_1 \cdot s + c_2 \cdot v + c_3 \cdot t

考虑误差​

上一节中默认将 r+altr+alt等效为 ∣q∣\lvert q\rvert，但实际上两者存在一定误差。

为了简化公式，现记误差值 r+altr+alt为 q^\hat{q}，可以得到：

c1=∣q^∣cos(∠q^os)∣s∣c2=∣q∣cos(∠qov)∣v∣c3=±q^2−∣q^∣2cos2(∠q^os)−∣q∣2cos2(∠qov)∣t∣≈±∣q^∣cos(∠q^ot)∣t∣\begin{aligned} c_1 = &\frac{\lvert \hat{q}\rvert cos(\angle \hat{q}os)}{\lvert s \rvert} \\ c_2 = &\frac{\lvert q\rvert cos(\angle qov)}{\lvert v \rvert} \\ c_3 =& \pm \frac{\sqrt{\hat{q}^2 - \lvert \hat{q} \rvert^2 cos^2(\angle \hat{q}os)-\lvert q \rvert^2 cos^2(\angle qov)}}{\lvert t \rvert} \\ \approx& \pm \frac{\lvert \hat{q}\rvert cos(\angle \hat{q}ot)}{\lvert t\rvert} \\ \end{aligned}

所以，

q≠c1⋅s+c2⋅v+c3⋅tq \ne c_1 \cdot s + c_2 \cdot v + c_3 \cdot t

通过上式得到的向量 q^k+1\hat q_{k+1}的模长介于 ∣q^k∣\lvert \hat q_k\rvert和 ∣q∣\lvert q\rvert之间，满足迭代收敛条件。

lat,lon,h->az_time->i,j​

通过指定的地面点坐标 RTR_T, 计算其对应的方位向时间 tazit_{azi}, 从而获取行列值的过程。

公式推导​

在地面点坐标和其他卫星参数已知的情况下, 方位向多普勒方程仅卫星位置矢量为未知条件, 且卫星位置矢量又是方位向时间的变量, 所以满足基本解算条件。

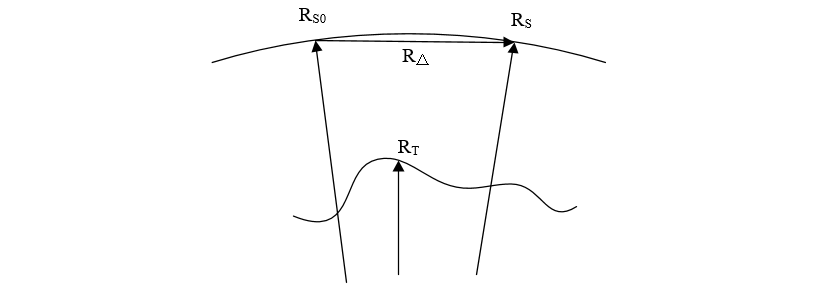
设卫星位置矢量的初始值为 RS0R_{S0}（通过初始时间t0t_0计算得到）, 满足多普勒频移公式的真实卫星位置矢量为 RS^\hat{R_S}, 初始值与真值的相对位置关系为

RS^=RS0+RΔ\hat{R_S} = R_{S0} + R_{\Delta}

三组位置矢量的相对位置关系如图所示，

位置矢量相对关系

因为位置矢量真值RS^\hat{R_S}与地面点坐标之间多普勒频移公式，所以将真值代入公式并简单整理后可得

fdλ2∣RS−RT∣=(RS−RT)VS\frac{f_d \lambda}{2}\lvert R_{S}-R_T\rvert = (R_{S}-R_T)V_S

将真值替换为初始值，可得

fdλ2∣RS0−RT∣=(RS0−RT)VS+RΔVS\frac{f_d \lambda}{2}\lvert R_{S0}-R_T\rvert = (R_{S0}-R_T)V_S + R_{\Delta}V_S

等号左侧，将∣RS−RT∣\lvert R_{S}-R_T\rvert近似替换为∣RS0−RT∣\lvert R_{S0}-R_T\rvert，虽然存在误差但通过迭代可以逐渐消除。整理后得到，

fdλ2∣RS0−RT∣−(RS0−RT)VS=RΔVS=∣RΔ∣∣VS∣cos⁡(0)=∣RΔ∣∣VS∣\begin{aligned} \frac{f_d \lambda}{2}\lvert R_{S0}-R_T\rvert - (R_{S0}-R_T)V_S =& R_{\Delta}V_S \\ =& \lvert R_{\Delta}\rvert \lvert V_S\rvert \cos(0) \\ =& \lvert R_{\Delta}\rvert \lvert V_S\rvert \end{aligned}

由 RS^\hat{R_S}、 RS0R_{S0}和 RΔR_{\Delta}的几何关系图可知 ∣RΔ∣=Δt∣VS∣\lvert R_{\Delta}\rvert = \Delta_t \lvert V_S\rvert, 代入公式可得，

Δt=12fdλ∣RS0−RT∣−(RS0−RT)VS∣VS∣2\Delta_t = \frac{\frac{1}{2}f_d \lambda\lvert R_{S0}-R_T\rvert - (R_{S0}-R_T)V_S}{{\lvert V_S\rvert}^2}

使用迭代值Δt\Delta_t，对初始时间t0t_0进行修正，多次迭代后即可得到正确结果。

代码实现​

double parameter_sar::get_state_t_iter(xyz target_point, bool& iter_succeed)
{
    int iter = 0;
    double t1 = get_azimuth_time(0);
    double alpha = 0.0;
    do{
        iter++;
        t1 += alpha;
        xyz pos  = get_state_pos(t1);
        xyz velo = get_state_velo(t1);

        xyz state_2_target = target_point - pos;
        double fd = 0;
        if(!azimuth_deskew){
            fd = this->get_fd(t1,state_2_target.norm());
        }
        double lambda = get_wave_length();
        alpha = -(fd * lambda / 2.*state_2_target.norm() - velo * state_2_target) / (velo * velo);

    }while(fabs(alpha)>0. && iter <= 16);

    if(fabs(alpha) < 0.00001){
        iter_succeed = true;
    }else{
        iter_succeed = false;
    }
    return t1;
}