影像重采样

双线性插值、三次卷积

双线性内插法

适用于规则点的插值。取插值点周围4个最近像元点，如图所示。

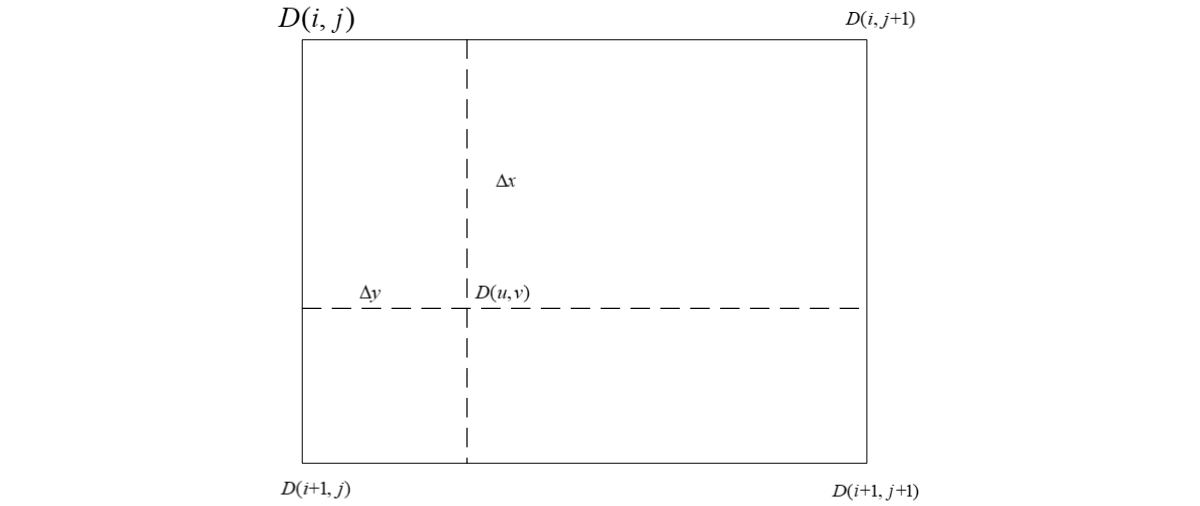
四个像元点应分布在插值点四周，像元点之间间隔为1像素，内插点 $(u,v)$的灰度值 $D(u,v)$为：

$$D(u,v)=[A][B][C]$$ $$A= \begin{bmatrix} \omega(\Delta x) & \omega(1-\Delta x) \end{bmatrix}$$ $$B=\begin{bmatrix} D(i,j) & D(i,j+1) \\ D(i+1,j) & D(i+1,j+1) \end{bmatrix}$$ $$C=\begin{bmatrix} \omega(\Delta y) \\ \omega(1-\Delta y) \end{bmatrix}$$ $$\omega(t)=\begin{cases} 1-\lvert t \rvert &, 0\leqslant \lvert t \rvert \leqslant1 \\ 0 &, \:\:another \end{cases}$$

整理得到，

$$D(u,v)= \begin{bmatrix} 1- \Delta x & \Delta x \end{bmatrix} \begin{bmatrix} D(i,j) & D(i,j+1) \\ D(i+1,j) & D(i+1,j+1) \end{bmatrix} \begin{bmatrix} 1- \Delta y \\ \Delta y \end{bmatrix} ,0\leqslant \Delta x,\Delta y \leqslant1$$

三次卷积插值

取插值点周围16个像元点，像元点间隔为1，如图所示。

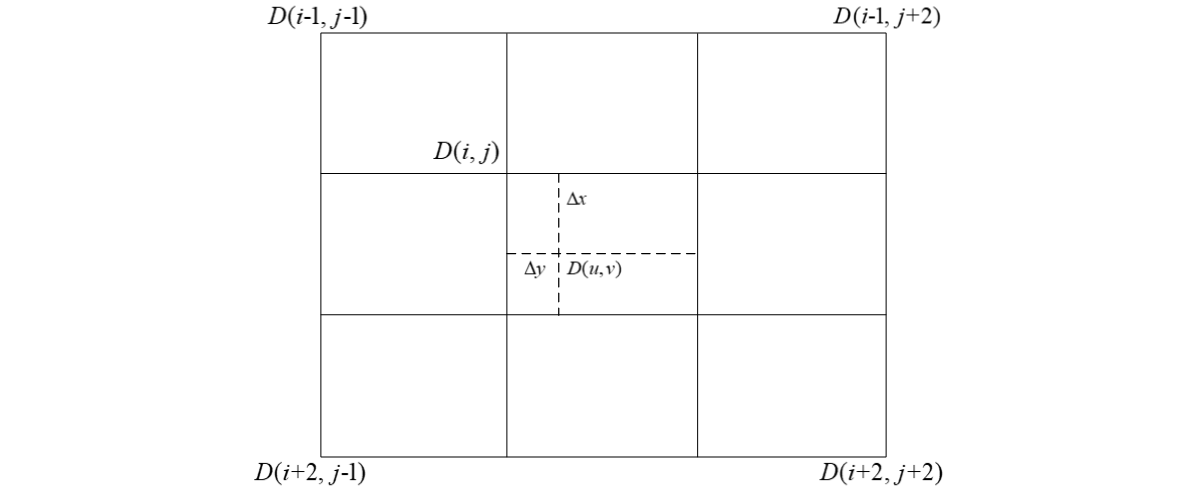
16个像元点应分布在插值点四周，像元点之间间隔为1像素，内插点 $(u,v)$的灰度值 $D(u,v)$ 为：

$$D(u,v)=[A][B][C]$$ $$A=\begin{bmatrix} \omega(1+\Delta x) & \omega(\Delta x) & \omega(1-\Delta x) & \omega(2-\Delta x) \end{bmatrix}$$ $$B=\begin{bmatrix} D(i-1,j-1) & D(i-1,j) & D(i-1,j+1) & D(i-1,j+2) \\ D( i ,j-1) & D( i ,j) & D( i ,j+1) & D( i ,j+2) \\ D(i+1,j-1) & D(i+1,j) & D(i+1,j+1) & D(i+1,j+2) \\ D(i+2,j-1) & D(i+2,j) & D(i+2,j+1) & D(i+2,j+2) \\ \end{bmatrix}$$ $$C=\begin{bmatrix} \omega(1+\Delta y) \\ \omega(\Delta y) \\ \omega(1-\Delta y) \\ \omega(2-\Delta y) \end{bmatrix}$$ $$\omega(t)=\begin{cases} 1-2{\lvert t\rvert}^2+{\lvert t\rvert}^3&,0 \leqslant \lvert t\rvert <1 \\ 4-8\lvert t\rvert+5{\lvert t\rvert}^2-{\lvert t\rvert}^3&,1 \leqslant \lvert t\rvert <2 \\ 0 &,\lvert t\rvert \geqslant 2 \end{cases}$$