Skip to main content

滤波

快速统计均值方差​

统计影像的均值和方差时，常规做法是先循环一遍计算均值，再循环一遍计算方差，但通过推导方差计算公式，可以简化上述操作，缩短统计耗时。

float mean = 0, std = 0;
for(int i=0; i < arr_size; i++){
    mean += arr[i];
    std += arr[i] * arr[i];
}
mean /= valid_num;
std = sqrtf(std / (valid_num-1) - valid_num / (valid_num-1) * mean * mean);

均值、方差的公式

xˉ=1n∑xiStd=1n−1∑(xi−xˉ)2=1n−1(∑xi2−nxˉ2)\begin{aligned} \bar{x} =& \frac{1}{n}\sum x_i \\ Std =& \sqrt{\frac{1}{n-1}\sum {(x_i - \bar{x})}^2} \\ =& \sqrt{\frac{1}{n-1}(\sum{{x_i}^2}-n{\bar{x}}^2)} \end{aligned}

方差的推导过程，

Std2=1n−1∑(xi−xˉ)2=1n−1∑(xi2−2xˉ⋅xi+xˉ2)=1n−1(∑xi2−2xˉ⋅∑xi+nxˉ2)=1n−1(∑xi2−2nxˉ2+nxˉ2)=1n−1(∑xi2−nxˉ2)⇒Std=1n−1(∑xi2−nxˉ2)\begin{aligned} &{Std}^2&=& \frac{1}{n-1}\sum {(x_i - \bar{x})}^2 \\ & &=& \frac{1}{n-1}\sum ({x_i}^2 - 2\bar{x}\cdot x_i+{\bar{x}}^2) \\ & &=& \frac{1}{n-1}(\sum {x_i}^2 - 2 \bar{x} \cdot \sum x_i + n {\bar{x}}^2) \\ & &=& \frac{1}{n-1}(\sum {x_i}^2 - 2 n {\bar{x}}^2 + n {\bar{x}}^2) \\ & &=& \frac{1}{n-1}(\sum {x_i}^2 - n {\bar{x}}^2) \\ \\ \Rarr & Std &=& \sqrt{\frac{1}{n-1}(\sum{{x_i}^2}-n{\bar{x}}^2)} \end{aligned}

Rolling Guidance Filter​

process

Qi Zhang, Xiaoyong Shen, Li Xu, and Jiaya Jia, ‘Rolling Guidance Filter’, ECCV 2014, pp. 812–830, 2014.

Step1: Small Structure Removal​

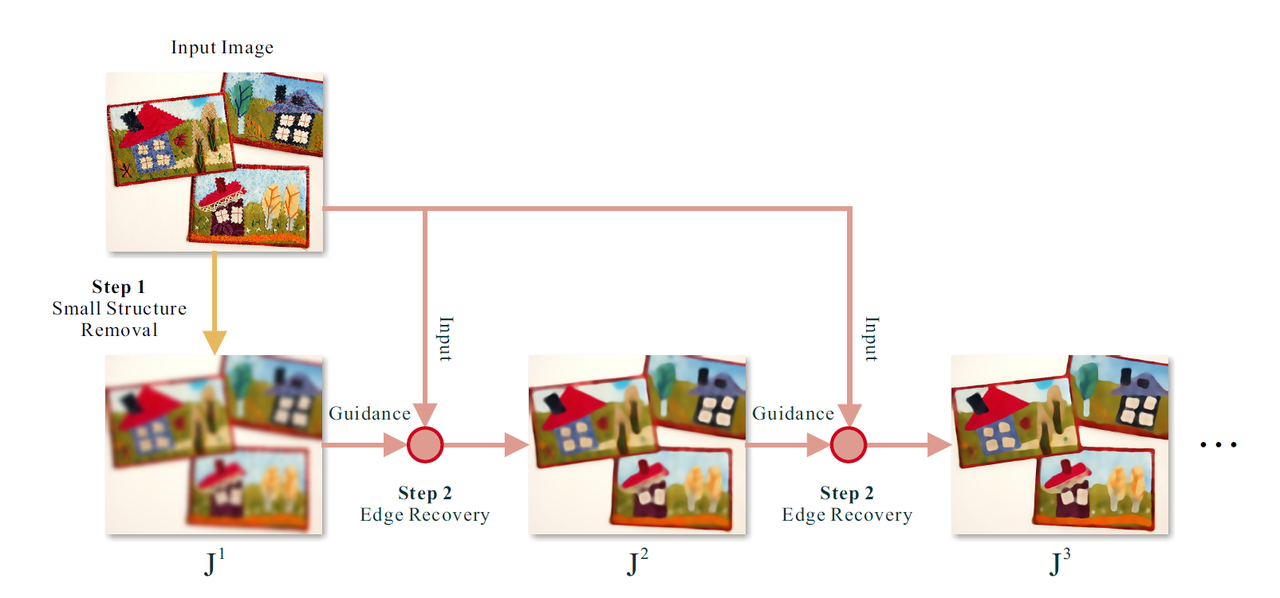
J1(p)=1Kp∑q∈N(p)exp⁡(−∥p−q∥22σs2)I(q)J_1(p)=\frac{1}{K_p}\displaystyle\sum_{q\in N(p)}\exp \bigg(-\frac{ {\|p-q\|}^2} {2\sigma_s^2}\bigg)I(q) Kp=∑q∈N(p)exp⁡(−∥p−q∥22σs2)K_p=\displaystyle\sum_{q\in N(p)}{\exp \big(-\frac{ {\|p-q\|}^2} {2\sigma_s^2}\big)}

其中， pp是待求点， qq是 pp周围的所有点的集合， II是原图像， σs2\sigma_s^2是标准偏差（ standard deviation）自己设定。通过这一步可以消除尺度小于 σs2\sigma_s^2的结构。

（This filter completely removes structures whose scale is smaller than σs2\sigma_s^2 as claimed in the scale space theory. It is implemented efficiently by separating kernels in perpendicular directions. Approximation by box filter is also feasible.）

Step2: Edge Recovery​

Jt+1(p)=1Kp∑q∈N(p)exp⁡(−∥p−q∥22σs2−∥Jt(p)−Jt(q)∥22σr2)I(q)J_{t+1}(p)=\frac{1}{K_p}\displaystyle\sum_{q\in N(p)}\exp \bigg(-\frac{ {\|p-q\|}^2}{2\sigma_s^2}-\frac{ {\|J_t(p)-J_t(q)\|}^2}{2\sigma_r^2}\bigg)I(q) Kp=∑q∈N(p)exp⁡(−∥p−q∥22σs2−∥Jt(p)−Jt(q)∥22σr2)K_p=\displaystyle\sum_{q\in N(p)}\exp \bigg(-\frac{ {\|p-q\|}^2}{2\sigma_s^2}-\frac{ {\|J_t(p)-J_t(q)\|}^2}{2\sigma_r^2}\bigg)

其中，pp是待求点，qq是 pp周围的所有点的集合， t=1,2,…,nt=1,2,…,n， II是原图像， σs2\sigma_s^2和 σr2\sigma_r^2分别控制时间权重和距离权重。

σs2\sigma_s^2 and σr2\sigma_r^2 control the spatial and range weights respectively

goldstein​

经典的频谱滤波

R. M. Goldstein and C. L. Werner, ‘Radar interferogram filtering for geophysical applications’, Geophysical Research Letters, vol. 25, no. 21, pp. 4035–4038, 1998, doi: 10.1029/1998GL900033

公式​

H(u,v)=S{∣Z(u,v)∣}α⋅Z(u,v)H(u,v) = {S\{ \lvert Z(u,v)\rvert \}}^\alpha \cdot Z(u,v)

派生方法​

优化方向主要有两种，一是优化平滑算子s{⋅}s\{\cdot\}，另一则是优化滤波系数⋅α{\cdot}^{\alpha}。

滤波系数​

baran滤波，使用相干图作为滤波系数

zhao滤波，使用伪相干图作为滤波系数

平滑算子​

某个软件，使用bessi0函数生成二维矩阵，在时域点乘后通过FFT转换到频域（时域点乘等于频域卷积），使用频域功率谱计算得到系数，将系数附加到频域后在通过IFFT转换回时域，完成滤波操作。

当然，老老实实写个均值滤波算子在频域做卷积运算，也是可以的，但效果确实不如上述方法。